Funções de Segundo Grau
1. O grau de uma função
O grau de uma variável independente é dado pelo seu expoente. Assim, as funções de segundo grau são dadas por um polinômio de segundo grau, e o grau do polinômio é dado pelo monômio de maior grau.
No dia-a-dia, há muitas situações
definidas pelas funções de segundo grau. A trajetória de uma bola
lançada para a frente é uma parábola. Se fizermos vários furos em várias
alturas num bote cheio de água, os pequenos jorros de água que saem
pelos furos descrevem parábolas. A antena parabólica tem a forma de
parábola, originando o seu nome.
2. Definição
Em geral, uma função quadrática ou polinomial do segundo grau é expressa da seguinte forma:
|
f (x) = ax2 + bx + c, onde a
|
Assim como os polinômios podem ser completos ou incompletos, temos funções de segundo grau incompletas, como:
|
f (x) = x2
f (x) = ax2 f (x) = ax2+ bx f (x) = ax2 + c |
Pode acontecer de o termo de segundo grau aparecer isoladamente, como na expressão geral y = ax2; acompanhado por um termo de primeiro grau, como no caso geral y = ax2 + bx; ou também unido a um termo independente ou a um valor constante, como em y = ax2 + c.
É comum pensarmos que a expressão algébrica
de uma função quadrática é mais complexa que a das funções lineares.
Normalmente, também supomos que sua representação gráfica é mais
complicada. Mas não é sempre assim. Além disso, os gráficos das funções
quadráticas são curvas muito interessantes, conhecidas como parábolas.
3. Representação gráfica da função y = ax2
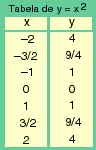
Como acontece com toda função,
para representá-la graficamente temos, antes, de construir uma tabela de
valores (Figura 3, ao lado).
Começamos representando a função quadrática y = x2, que é a expressão mais simples da função polinomial de segundo grau.
Se unirmos os pontos com uma linha contínua, o resultado é uma parábola, como mostra a Figura 4, abaixo:
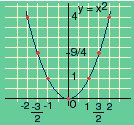
Observando atentamente a tabela de valores e a representação gráfica da função y = x2 vamos perceber que o eixo Y, das ordenadas, é o eixo de simetria do gráfico.
|
Além disso, o ponto mais baixo da curva (aquele em que a curva se intercepta com o eixo Y) é o ponto de coordenadas (0, 0). Este ponto é conhecido como vértice da parábola.
|
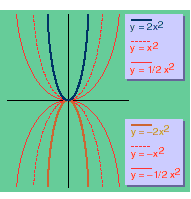
Na Figura 5, ao lado, estão as representações gráficas de várias funções que têm como expressão geral y = ax2.
Observando com atenção a Figura 5 podemos afirmar:
• O eixo de simetria de todos os gráficos é o eixo Y.
Como x2 = (– x)2, a curva é simétrica em relação ao eixo das ordenadas.
Como x2 = (– x)2, a curva é simétrica em relação ao eixo das ordenadas.
• A função y = x2 é crescente para x > xv e decrescente para x < xv. Trata-se de uma função contínua, pois para pequenas variações de x correspondem pequenas variações de y.
• Todas as curvas têm o vértice no ponto (0,0).
• Todas as curvas que estão no semiplano de ordenadas positivas, com exceção do vértice V (0,0), têm ponto de mínimo que é o próprio vértice.
• Todas as curvas que estão no semiplano de ordenadas negativas, com exceção do vértice V (0,0), têm ponto de máximo que é o próprio vértice.
• Se o valor de a for positivo, os ramos da parábola se dirigem para cima. Ao contrário, se a for negativo, os ramos se dirigem para baixo. Dessa forma, o sinal do coeficiente determina a orientação da parábola:
|
a > 0, a parábola abre-se para valores positivos de y.
a < 0, a parábola abre-se para valores negativos de y.
|
|
•
|
À medida que aumenta o valor absoluto de a, a parábola é mais fechada, isto é, os ramos ficam mais próximos do eixo de simetria: quanto maior |a|, mais a parábola se fecha.
|
|
•
|
Os gráficos de y = ax2 e y = –ax2 são simétricos entre si com relação ao eixo X, das abscissas.
|

Nenhum comentário:
Postar um comentário